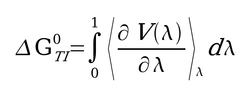Difference between revisions of "AMBER TI Tutorials"
Stonybrook (talk | contribs) (→Start Structures Results and scripts preparation) |
(→Thermodynamic cycle and Method) |
||
| (39 intermediate revisions by one other user not shown) | |||
| Line 7: | Line 7: | ||
==Thermodynamic cycle and Method== | ==Thermodynamic cycle and Method== | ||
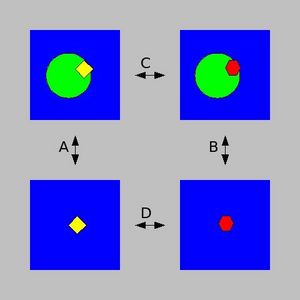
| − | TI calculations compute the free energy difference between two states A and B by coupling them via a parameters λ that serves as an additional, nonspatial coordinate. This λ formalism allows the free energy difference between the states to be computed as | + | [[Image:Thermodynamic Integration cycle.jpg|left|thumb|300px|To calculate the binding energy difference between two ligands, look at the thermodynamic cycle on the left.]] |
| − | + | TI calculations compute the free energy difference between two states A and B by coupling them via a parameters λ that serves as an additional, nonspatial coordinate. This λ formalism allows the free energy difference between the states to be computed as in the equation shown on the right. | |
| − | + | [[Image:Picture1.jpg|thumb|250px|λ formalism for thermodynamic integration]] | |
| − | |||
| − | [[Image: | ||
From the pictures above, you can see that Processes A and B represent the binding of two different ligands to a protein, while processes C and D are transformations from one ligand to the other while it is bound to the protein (C) or simply solvated in water (D). | From the pictures above, you can see that Processes A and B represent the binding of two different ligands to a protein, while processes C and D are transformations from one ligand to the other while it is bound to the protein (C) or simply solvated in water (D). | ||
| Line 37: | Line 35: | ||
source leaprc.gaff | source leaprc.gaff | ||
loadoff benz.lib | loadoff benz.lib | ||
| − | + | ||
complex = loadpdb 181L_mod.pdb | complex = loadpdb 181L_mod.pdb | ||
solvatebox complex TIP3PBOX 12 | solvatebox complex TIP3PBOX 12 | ||
addions complex Cl- 0 | addions complex Cl- 0 | ||
savepdb complex complex.pdb | savepdb complex complex.pdb | ||
| − | + | ||
ligand = copy BNZ | ligand = copy BNZ | ||
solvatebox ligand TIP3PBOX 12 | solvatebox ligand TIP3PBOX 12 | ||
| Line 55: | Line 53: | ||
loadoff benz.lib | loadoff benz.lib | ||
loadoff phen.lib | loadoff phen.lib | ||
| − | + | ||
complex = loadpdb complex.pdb | complex = loadpdb complex.pdb | ||
setbox complex vdw | setbox complex vdw | ||
savepdb complex t4_bnz_leap.pdb | savepdb complex t4_bnz_leap.pdb | ||
saveamberparm complex t4_bnz.prm t4_bnz.rst | saveamberparm complex t4_bnz.prm t4_bnz.rst | ||
| − | + | ||
ligand = loadpdb ligand.pdb | ligand = loadpdb ligand.pdb | ||
setbox ligand vdw | setbox ligand vdw | ||
savepdb ligand bnz_leap.pdb | savepdb ligand bnz_leap.pdb | ||
saveamberparm ligand bnz.prm bnz.rst | saveamberparm ligand bnz.prm bnz.rst | ||
| − | + | ||
complex = loadpdb t4_phn.pdb | complex = loadpdb t4_phn.pdb | ||
setbox complex vdw | setbox complex vdw | ||
savepdb complex t4_phn_leap.pdb | savepdb complex t4_phn_leap.pdb | ||
saveamberparm complex t4_phn.prm t4_phn.rst | saveamberparm complex t4_phn.prm t4_phn.rst | ||
| − | + | ||
ligand = loadpdb phn.pdb | ligand = loadpdb phn.pdb | ||
setbox ligand vdw | setbox ligand vdw | ||
| Line 80: | Line 78: | ||
After the following steps, you should already have 4 sets of starting structures for the system. Now we should focus on the scripts used to run the thermodynamics integration. | After the following steps, you should already have 4 sets of starting structures for the system. Now we should focus on the scripts used to run the thermodynamics integration. | ||
| − | you can get these sets of files from Shun, or download them from the [http://ambermd.org/tutorials/advanced/tutorial9/setup.html Thomas site] | + | you can get these sets of files from Shun, or download them from the [http://ambermd.org/tutorials/advanced/tutorial9/setup.html Thomas site]. |
There are totally 6 directories for you to make a 3-step change in 2 different environments. Moreover, '''in each directory, you should do 3 steps for a complete simulation: minimization, equilibration, production.''' | There are totally 6 directories for you to make a 3-step change in 2 different environments. Moreover, '''in each directory, you should do 3 steps for a complete simulation: minimization, equilibration, production.''' | ||
| + | |||
| + | In this case, we will do: | ||
| + | *500 steps of steepest descent minimization (the only kind working with TI) | ||
| + | *50 ps of density equilibration (equilibrating T and δ at the same time is not very good form, but we'll get away with it here | ||
| + | *200 ps of NPT production MD to collect dV/dλ data | ||
| + | |||
| + | The following is a short description of the script: | ||
| + | |||
| + | '''minimization: ''' | ||
| + | COMMENT: this is a minimization | ||
| + | &cntrl | ||
| + | imin = 1, ntx = 1, | ||
| + | maxcyc=500, | ||
| + | ntpr = 100, | ||
| + | ntf = 2, ntc = 2, | ||
| + | ntb = 1, cut = 9.0, | ||
| + | icfe=1, clambda = 0.${X}, | ||
| + | ifsc=0, | ||
| + | crgmask='${mask0}', | ||
| + | &end | ||
| + | |||
| + | '''equilibration''' | ||
| + | density equilibration | ||
| + | &cntrl | ||
| + | imin = 0, ntx = 1, irest = 0, | ||
| + | ntpr = 2500, ntwr = 10000, ntwx = 0, | ||
| + | ntf = 2, ntc = 2, | ||
| + | ntb = 2, cut = 9.0, | ||
| + | nstlim = 25000, dt = 0.002, | ||
| + | temp0 = 300.0, ntt = 3, gamma_ln = 5, | ||
| + | ntp = 1, pres0 = 1.0, taup = 0.2, | ||
| + | icfe=1, clambda = 0.${X}, | ||
| + | ifsc=0, | ||
| + | crgmask='${mask0}', | ||
| + | &end | ||
| + | |||
| + | |||
| + | '''production''' | ||
| + | NPT production | ||
| + | &cntrl | ||
| + | imin = 0, ntx = 5, irest = 1, | ||
| + | ntpr = 10000, ntwr = 100000, ntwx = 10000, | ||
| + | ntf = 2, ntc = 2, | ||
| + | ntb = 2, cut = 9.0, | ||
| + | nstlim = 100000, dt = 0.002, | ||
| + | temp0 = 300.0, ntt = 3, gamma_ln = 2, | ||
| + | ntp = 1, pres0 = 1.0, taup = 2.0, | ||
| + | icfe=1, clambda = 0.${X}, | ||
| + | ifsc=0, | ||
| + | crgmask='${mask0}', | ||
| + | &end | ||
| + | |||
| + | Remember to change the masks in your actual scripts. The masks here make it easy to reuse the scripts. | ||
| + | |||
| + | When the softcore potential algorithms are activated, the scripts are a little different. | ||
==Setup and run MD== | ==Setup and run MD== | ||
I would create 6 directories to run the Thermodynamics Integration Molecular Dynamics separately. | I would create 6 directories to run the Thermodynamics Integration Molecular Dynamics separately. | ||
| − | '''3 steps: removing the charges from benzene, VDW change from benzene to phenol, adding the charges to phenol. 2 environments: unbound water environment and bound with T4 L99A environment.''' | + | '''3 steps: removing the charges from benzene, VDW change from benzene to phenol, adding the charges to phenol. ''' |
| + | |||
| + | '''2 environments: unbound water environment and bound with T4 L99A environment.''' | ||
For the second step which is VDW change from benzene to phenol, some important changes have been made. In AMBER 10, a new kind of method is used: softcore potentials algorithm. Using this algorithm removes the requirement to prepare "dummy" atoms and allows two parameter/top files to have different atoms. | For the second step which is VDW change from benzene to phenol, some important changes have been made. In AMBER 10, a new kind of method is used: softcore potentials algorithm. Using this algorithm removes the requirement to prepare "dummy" atoms and allows two parameter/top files to have different atoms. | ||
| Line 101: | Line 156: | ||
* ntf should equal 1 for all softcore part. Otherwise, there would be errors or crashes in the SANDER module. | * ntf should equal 1 for all softcore part. Otherwise, there would be errors or crashes in the SANDER module. | ||
| − | '''the bash scripts for running the simulations are listed below:''' | + | * Set proper time for the simulations to run. Generally, TIMD will take a lot of time. The with_t4 environment will take much more time for running a simulation. In this example, we use the following setups as Thomas: |
| + | **500 steps of steepest descent minimization (the only kind working with TI) | ||
| + | **50 ps of density equilibration (equilibrating T and δ at the same time is not very good form, but we'll get away with it here | ||
| + | **200 ps of NPT production MD to collect dV/dλ data | ||
| + | So the total computing time on seawulf is about 4 hours for no_t4_part, 48 hours for with_t4_part. | ||
| + | |||
| + | |||
| + | |||
| + | '''the bash scripts for running the simulations on the seawulf are listed below:''' | ||
| − | no_t4_step1: | + | no_t4_step1: [[no_t4_step1_inputgen.bash]] |
| − | no_t4_step2: | + | no_t4_step2: [[no_t4_step2_min.bash]], [[no_t4_step2_equiprod.bash]] |
| − | no_t4_step3: | + | no_t4_step3: [[no_t4_step3_inputgen.bash]] |
| − | with_t4_step1: | + | with_t4_step1: [[with_t4_step1_inputgen.bash]] |
| − | with_t4_step2: | + | with_t4_step2: [[with_t4_step2_min.bash]], [[with_t4_step2_equiprod.bash]] |
| − | with_t4_step3: | + | with_t4_step3: [[with_t4_step3_inputgen.bash]] |
==Post-processing== | ==Post-processing== | ||
After running the simulations on the seawulf cluster, you still have plenty of work to do. The analyze of the data is not so straight and you need to write linux scripts using python or perl to extract the data. | After running the simulations on the seawulf cluster, you still have plenty of work to do. The analyze of the data is not so straight and you need to write linux scripts using python or perl to extract the data. | ||
| − | I write a python extraction scripts myself to extract the data DVDL and rms data like the following format: | + | I write a python extraction scripts myself to extract the data DVDL and rms data like the following file TIMD_extraction.py. Your should read and know how it works: in that case, you could know how to modify it for your use. |
| + | |||
| + | For the integration calculation, Thomas has a PERL script. I have rewritten it by python. You can use or modify both of them according to your needs. The basic direction for writing the integration scripts is to get the width or weight of each lambda value; then you can use the width to calculate everything. Notice that the DV/DL values for Lambda 0 and 1 are just estimations from the adjacent points. | ||
| + | |||
| + | some scripts for analysis: | ||
| + | * Extracts data from output files: [[TIMD_extraction.py]] | ||
| + | '''To use the extraction script, read the instructions in the code carefully, and set the filename variable as you need. ''' | ||
| + | * Preparation of data for integration: [[TIMD_integration_prep.py]] | ||
| + | '''Get the lambda, DVDL, and rms information from the extraction report data; output in the format that could be used for integration''' | ||
| + | * Integration part for the data: | ||
| + | **Thomas's integration perl script: [[integration.pl]] | ||
| + | **Shun's integration python script: [[TIMD_integration.py]] | ||
| + | '''Integration is done using simple error estimation, you can modify the script to use Gaussian error estimation. ''' | ||
| + | |||
| + | ==Graphs From the Data== | ||
| + | Here I will show you the DVDL-lambda data I get from my simulation results. The graph is according to the format of Thomas' tutorials. | ||
| + | [[Image:T4_TIMD_results.jpg]] | ||
| + | |||
| + | [[Image:T4_data_result.jpg]] | ||
| + | |||
| + | This is the final result of my simulation. | ||
| + | |||
| + | You would find that the main energy difference comes from the step2. This is an interesting phenomenon. Thomas' comment: "One would have expected that the loss of solvation on the polar hydroxyl group might strongly influence the relative binding free energies, but from this calculations, the main difference seems to be the sterical effect of accomodating the bulkier hydroxyl group in the binding site, with electrostatics playing a minor role. This result might however change if the calculation would be refined further." | ||
| + | |||
| + | You can make your own comment from the results. The ability to analyze data is as important as the ability to generate data. == | ||
Latest revision as of 17:50, 7 June 2010
Contents
Introduction to TIMD
This is a TIMD tutorial based on the tutorial written by Thomas Steinbrecher. But some important changes have been made to suit the current AMBER 10 version according to Miranda's tutorial from Simmerling's lab.
And this is my own version of TIMD of the T4-L99A enzyme, the results are a little different from Thomas' results due to some changes in the parameters. Always remember that the experimental value is the absolute criteria.
In this tutorial, free energy calculations will be used to calculate the relative binding free energy of two simple ligands, benzene and phenol to the T4-lysozyme mutant L99A. Free energies will be computed by using the thermodynamic integration facilities of the sander program. A modified van-der-Waals equation (softcore potentials) are used to ensure smooth free energy curves.
Thermodynamic cycle and Method
TI calculations compute the free energy difference between two states A and B by coupling them via a parameters λ that serves as an additional, nonspatial coordinate. This λ formalism allows the free energy difference between the states to be computed as in the equation shown on the right.
From the pictures above, you can see that Processes A and B represent the binding of two different ligands to a protein, while processes C and D are transformations from one ligand to the other while it is bound to the protein (C) or simply solvated in water (D).
Since Δ GC-Δ GD = Δ GA-Δ GB, TI calculations can be used to compute relative binding free energies, making them useful tools in drug design or lead optimization applications.
Preparation for setup of the T4 L99A System
The two ligands were sketched and parametrized with gaff atom types and resp charges were generated using antechamber on gaussian03 output files. (Please refer to a basic AMBER tutorial on how to use the antechamber tools to parametrize a ligand. The benzene and phenol molecules were saved in two OFF-libraries (benz.lib and phen.lib) for further use. The screenshot shows that C6 was selected as the position bearing the hydroxyl group in phenol.
You can get the OFF-libraries from Shun or just download it from the following links:benz.lib and phen.lib.
We are going to use the X-ray structure of T4-L99A from the pdb (after stripping water molecules and unneeded heteroatoms from it: pdb file) as basis to set up our simulation files. Generally, you can strip the waters and other unneeded molecules in another software, but here the modified pdb file is already provided.
We will use two runs of leap to produce four sets of parameter and restart files, containing both ligands in the protein bound and solvated states.
Notice if there are sharp changes in the TIMD process, more sets of parameter and restart files are required(generally 6 sets). For example, in Miranda's tutorial, she has 3 sets of topology/coordinate files for each transformation: two 'original' endpoint files generated directly from crystal/MD structures, one 'fake' endpoint file generated by mutating one 'original' endpoint file. Thus totally 6 sets of files for her tutorial.
tleap to generate sets of parameter and restart files
We will use two runs of leap to produce four set of parameter and restart files, containing both ligands in the protein bound and solvated states. The first leap run (input file) will produce pdb files of the solvated und neutralized benzene complex and of the benzene ligand in water (complex.pdb and ligand.pdb). From these two additional pdb files are made by renaming the BNZ molecule to PHN and deleting H6 (t4_phn.pdb and phn.pdb).
The script for first tleap run:
source leaprc.ff03 source leaprc.gaff loadoff benz.lib complex = loadpdb 181L_mod.pdb solvatebox complex TIP3PBOX 12 addions complex Cl- 0 savepdb complex complex.pdb ligand = copy BNZ solvatebox ligand TIP3PBOX 12 savepdb ligand ligand.pdb
These four pdb files are then used in a second leap run (input file) to generate the *.prm and *.rst files. This yields 4 parameter and 4 rst files.
The script for second tleap run:
source leaprc.ff03 source leaprc.gaff loadoff benz.lib loadoff phen.lib complex = loadpdb complex.pdb setbox complex vdw savepdb complex t4_bnz_leap.pdb saveamberparm complex t4_bnz.prm t4_bnz.rst ligand = loadpdb ligand.pdb setbox ligand vdw savepdb ligand bnz_leap.pdb saveamberparm ligand bnz.prm bnz.rst complex = loadpdb t4_phn.pdb setbox complex vdw savepdb complex t4_phn_leap.pdb saveamberparm complex t4_phn.prm t4_phn.rst ligand = loadpdb phn.pdb setbox ligand vdw savepdb ligand phn_leap.pdb saveamberparm ligand phn.prm phn.rst
Start Structures Results and scripts preparation
After the following steps, you should already have 4 sets of starting structures for the system. Now we should focus on the scripts used to run the thermodynamics integration.
you can get these sets of files from Shun, or download them from the Thomas site.
There are totally 6 directories for you to make a 3-step change in 2 different environments. Moreover, in each directory, you should do 3 steps for a complete simulation: minimization, equilibration, production.
In this case, we will do:
- 500 steps of steepest descent minimization (the only kind working with TI)
- 50 ps of density equilibration (equilibrating T and δ at the same time is not very good form, but we'll get away with it here
- 200 ps of NPT production MD to collect dV/dλ data
The following is a short description of the script:
minimization:
COMMENT: this is a minimization
&cntrl
imin = 1, ntx = 1,
maxcyc=500,
ntpr = 100,
ntf = 2, ntc = 2,
ntb = 1, cut = 9.0,
icfe=1, clambda = 0.${X},
ifsc=0,
crgmask='${mask0}',
&end
equilibration
density equilibration
&cntrl
imin = 0, ntx = 1, irest = 0,
ntpr = 2500, ntwr = 10000, ntwx = 0,
ntf = 2, ntc = 2,
ntb = 2, cut = 9.0,
nstlim = 25000, dt = 0.002,
temp0 = 300.0, ntt = 3, gamma_ln = 5,
ntp = 1, pres0 = 1.0, taup = 0.2,
icfe=1, clambda = 0.${X},
ifsc=0,
crgmask='${mask0}',
&end
production
NPT production
&cntrl
imin = 0, ntx = 5, irest = 1,
ntpr = 10000, ntwr = 100000, ntwx = 10000,
ntf = 2, ntc = 2,
ntb = 2, cut = 9.0,
nstlim = 100000, dt = 0.002,
temp0 = 300.0, ntt = 3, gamma_ln = 2,
ntp = 1, pres0 = 1.0, taup = 2.0,
icfe=1, clambda = 0.${X},
ifsc=0,
crgmask='${mask0}',
&end
Remember to change the masks in your actual scripts. The masks here make it easy to reuse the scripts.
When the softcore potential algorithms are activated, the scripts are a little different.
Setup and run MD
I would create 6 directories to run the Thermodynamics Integration Molecular Dynamics separately.
3 steps: removing the charges from benzene, VDW change from benzene to phenol, adding the charges to phenol.
2 environments: unbound water environment and bound with T4 L99A environment.
For the second step which is VDW change from benzene to phenol, some important changes have been made. In AMBER 10, a new kind of method is used: softcore potentials algorithm. Using this algorithm removes the requirement to prepare "dummy" atoms and allows two parameter/top files to have different atoms.
Several things to notice when run the molecular dynamics:
- you can use different numbers of windows. But when you use the new windows, the original windows' simulation data could also be used.
- running the minimization separatesly for the VDW change step. Because in this step, only 2 processors could be used to run the minimizations. You can use more processors for the equilibrium and production steps.
- Make sure to always use Langevin when you are applying soft core potential, for this is a requirement in AMBER manual.
- ntf should equal 1 for all softcore part. Otherwise, there would be errors or crashes in the SANDER module.
- Set proper time for the simulations to run. Generally, TIMD will take a lot of time. The with_t4 environment will take much more time for running a simulation. In this example, we use the following setups as Thomas:
- 500 steps of steepest descent minimization (the only kind working with TI)
- 50 ps of density equilibration (equilibrating T and δ at the same time is not very good form, but we'll get away with it here
- 200 ps of NPT production MD to collect dV/dλ data
So the total computing time on seawulf is about 4 hours for no_t4_part, 48 hours for with_t4_part.
the bash scripts for running the simulations on the seawulf are listed below:
no_t4_step1: no_t4_step1_inputgen.bash
no_t4_step2: no_t4_step2_min.bash, no_t4_step2_equiprod.bash
no_t4_step3: no_t4_step3_inputgen.bash
with_t4_step1: with_t4_step1_inputgen.bash
with_t4_step2: with_t4_step2_min.bash, with_t4_step2_equiprod.bash
with_t4_step3: with_t4_step3_inputgen.bash
Post-processing
After running the simulations on the seawulf cluster, you still have plenty of work to do. The analyze of the data is not so straight and you need to write linux scripts using python or perl to extract the data.
I write a python extraction scripts myself to extract the data DVDL and rms data like the following file TIMD_extraction.py. Your should read and know how it works: in that case, you could know how to modify it for your use.
For the integration calculation, Thomas has a PERL script. I have rewritten it by python. You can use or modify both of them according to your needs. The basic direction for writing the integration scripts is to get the width or weight of each lambda value; then you can use the width to calculate everything. Notice that the DV/DL values for Lambda 0 and 1 are just estimations from the adjacent points.
some scripts for analysis:
- Extracts data from output files: TIMD_extraction.py
To use the extraction script, read the instructions in the code carefully, and set the filename variable as you need.
- Preparation of data for integration: TIMD_integration_prep.py
Get the lambda, DVDL, and rms information from the extraction report data; output in the format that could be used for integration
- Integration part for the data:
- Thomas's integration perl script: integration.pl
- Shun's integration python script: TIMD_integration.py
Integration is done using simple error estimation, you can modify the script to use Gaussian error estimation.
Graphs From the Data
Here I will show you the DVDL-lambda data I get from my simulation results. The graph is according to the format of Thomas' tutorials.

This is the final result of my simulation.
You would find that the main energy difference comes from the step2. This is an interesting phenomenon. Thomas' comment: "One would have expected that the loss of solvation on the polar hydroxyl group might strongly influence the relative binding free energies, but from this calculations, the main difference seems to be the sterical effect of accomodating the bulkier hydroxyl group in the binding site, with electrostatics playing a minor role. This result might however change if the calculation would be refined further."
You can make your own comment from the results. The ability to analyze data is as important as the ability to generate data. ==